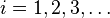La longitud de una curva plana se puede aproximar al sumar pequeños segmentos de recta que se ajusten a la curva, esta aproximación será más ajustada entre más segmentos sean y a la vez sean lo más pequeño posible.
Definición:
Si la primera derivada de una función es continua en [a,b] se dice que es suave y su gráfica es una curva suave.
En matemática, la longitud de arco, también llamada rectificación de una curva, es la medida de la distancia o camino recorrido a lo largo de una curva o dimensión lineal. Históricamente, ha sido difícil determinar esta longitud en segmentos irregulares; aunque fueron usados varios métodos para curvas específicas, la llegada del cálculo trajo consigo la fórmula general para obtener soluciones cerradas para algunos casos.
A través de la historia de las matemáticas, grandes pensadores consideraron imposible calcular la longitud de un arco irregular. Aunque Arquímedes había descubierto una aproximación rectangularpara calcular el área bajo una curva con un método de agotamiento, pocos creyeron que era posible que una curva tuviese una longitud definida, como las líneas rectas. Las primeras mediciones se hicieron posibles, como ya es común en el cálculo, a través de aproximaciones: los matemáticos de la época trazaban un polígono dentro de la curva, y calculaban la longitud de los lados de éste para obtener un valor aproximado de la longitud de la curva. Mientras se usaban más segmentos, disminuyendo la longitud de cada uno, se obtenía una aproximación cada vez mejor.
Suponiendo que se tiene una curva rectificable cualquiera, determinada por una función , y suponiendo que se quiere aproximar la longitud del arco de curva s que va desde un punto a a uno b. Con este propósito es posible diseñar una serie de triángulos rectángulos cuyas hipotenusas concatenadas "cubran" el arco de curva elegido tal como se ve en la figura. Para hacer a este método "más funcional" también se puede exigir que las bases de todos aquellos triángulos sean iguales a Δx, de manera que para cada uno existirá un cateto Δy asociado, dependiendo del tipo de curva y del arco elegido, siendo entonces cada hipotenusa.
PRACTICA LONGITUD DE CURVAS
PRACTICA LONGITUD DE CURVAS
REFERENCIA:
http://es.wikipedia.org/wiki/Longitud_de_arco
EJEMPLO VIDEO:
http://www.youtube.com/watch?v=QLFhBPOtF4s